Swing Distillation: A Privacy-Preserving Knowledge Distillation Framework

Metadata

• Authors: [[Junzhuo Li]], [[Xinwei Wu]], [[Weilong Dong]], [[Shuangzhi Wu]], [[Chao Bian]], [[Deyi Xiong]]
• Date: [[2022-12-16]] NIPS 2022
• Date Added: [[2023-12-12]]
• URL: http://arxiv.org/abs/2212.08349
• Topics: [[privacy]]
• Tags: #Computer-Science—Machine-Learning, #Computer-Science—Artificial-Intelligence, #Computer-Science—Cryptography-and-Security, #Computer-Science—Computation-and-Language, #/unread, #zotero, #literature-notes, #reference
• PDF Attachments
  • Li 等 - 2022 - Swing Distillation A Privacy-Preserving Knowledge.pdf

Abstract

Knowledge distillation (KD) has been widely used for model compression and knowledge transfer. Typically, a big teacher model trained on sufficient data transfers knowledge to a small student model. However, despite the success of KD, little effort has been made to study whether KD leaks the training data of the teacher model. In this paper, we experimentally reveal that KD suffers from the risk of privacy leakage. To alleviate this issue, we propose a novel knowledge distillation method, swing distillation, which can effectively protect the private information of the teacher model from flowing to the student model. In our framework, the temperature coefficient is dynamically and adaptively adjusted according to the degree of private information contained in the data, rather than a predefined constant hyperparameter. It assigns different temperatures to tokens according to the likelihood that a token in a position contains private information. In addition, we inject noise into soft targets provided to the student model, in order to avoid unshielded knowledge transfer. Experiments on multiple datasets and tasks demonstrate that the proposed swing distillation can significantly reduce (by over 80% in terms of canary exposure) the risk of privacy leakage in comparison to KD with competitive or better performance. Furthermore, swing distillation is robust against the increasing privacy budget.

Zotero links

• Local library
• Cloud library

Contribution

提出新的蒸馏方法，能够保护 teacher model 的训练数据。主要包括：

1. 动态温度
   构建敏感词字典，在蒸馏的时候，server 遇到 public dataset 中出现这类词 input，则对这些词的 softmax之后，给予KD一个较大的温度，想要把敏感词附近的概率分布变得平坦，使得不泄漏这部分的隐私信息。也就是让KD遇到敏感词时，根据敏感字典与敏感词的匹配程度，敏感程度越高，给予越高的蒸馏温度。
2. soft target 保护
   与传统的给传输的knowledge加噪声不同，此处只是对概率分布中较大的 Top-K 个概率加噪声，其他分类概率不变，这样既能保证保护了要预测的分类，又能添加不多的噪声，不影响性能。

Preliminary

当学生模型遇到攻击时，有一定的概率从教师数据集中生成发件人姓名。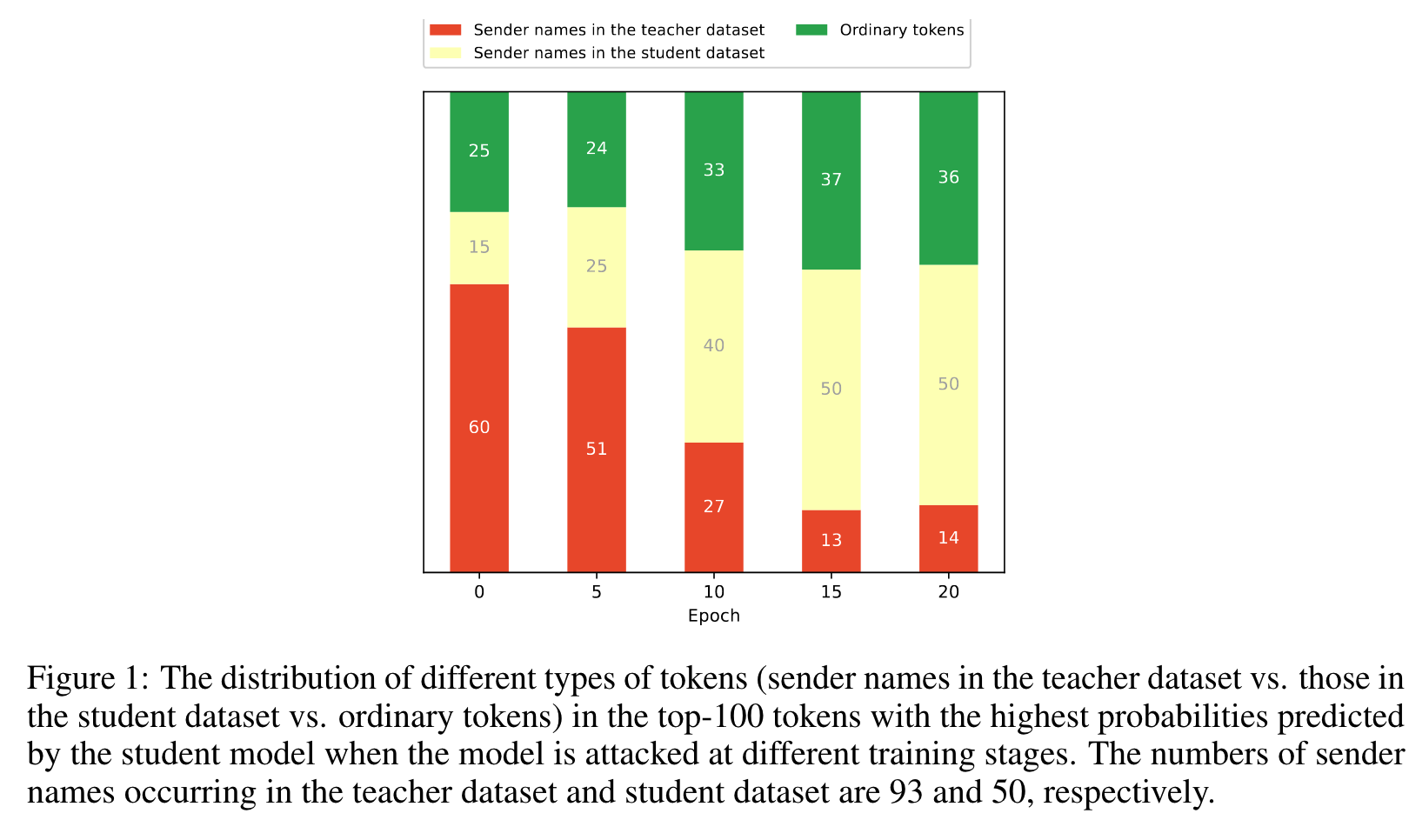

即使教师数据集中的邮件发件人姓名在学生数据集中完全不存在，提炼后的学生模型仍有很高的概率输出这些姓名。
我们使用 “这封邮件是由……撰写的 “作为提示，检查学生模型是否会输出插入教师数据集中占位符的发件人姓名。图 1 显示了学生模型在得到这一提示时预测出的前 100 个词块的分布情况。可以看出，学生模型在遇到攻击时，有一定概率从教师数据集中生成发件人姓名。由于这些名字并不存在于学生数据集中，而只出现在教师数据集中，因此这些结果强烈表明 KD 存在向学生模型泄露私人信息的风险。
当模型在不同训练阶段受到攻击时，学生模型预测概率最高的前 100 个令牌中不同类型令牌（教师数据集中的发件人姓名与学生数据集中的发件人姓名以及普通令牌）的分布情况。教师数据集和学生数据集中出现的发件人姓名数量分别为 93 个和 50 个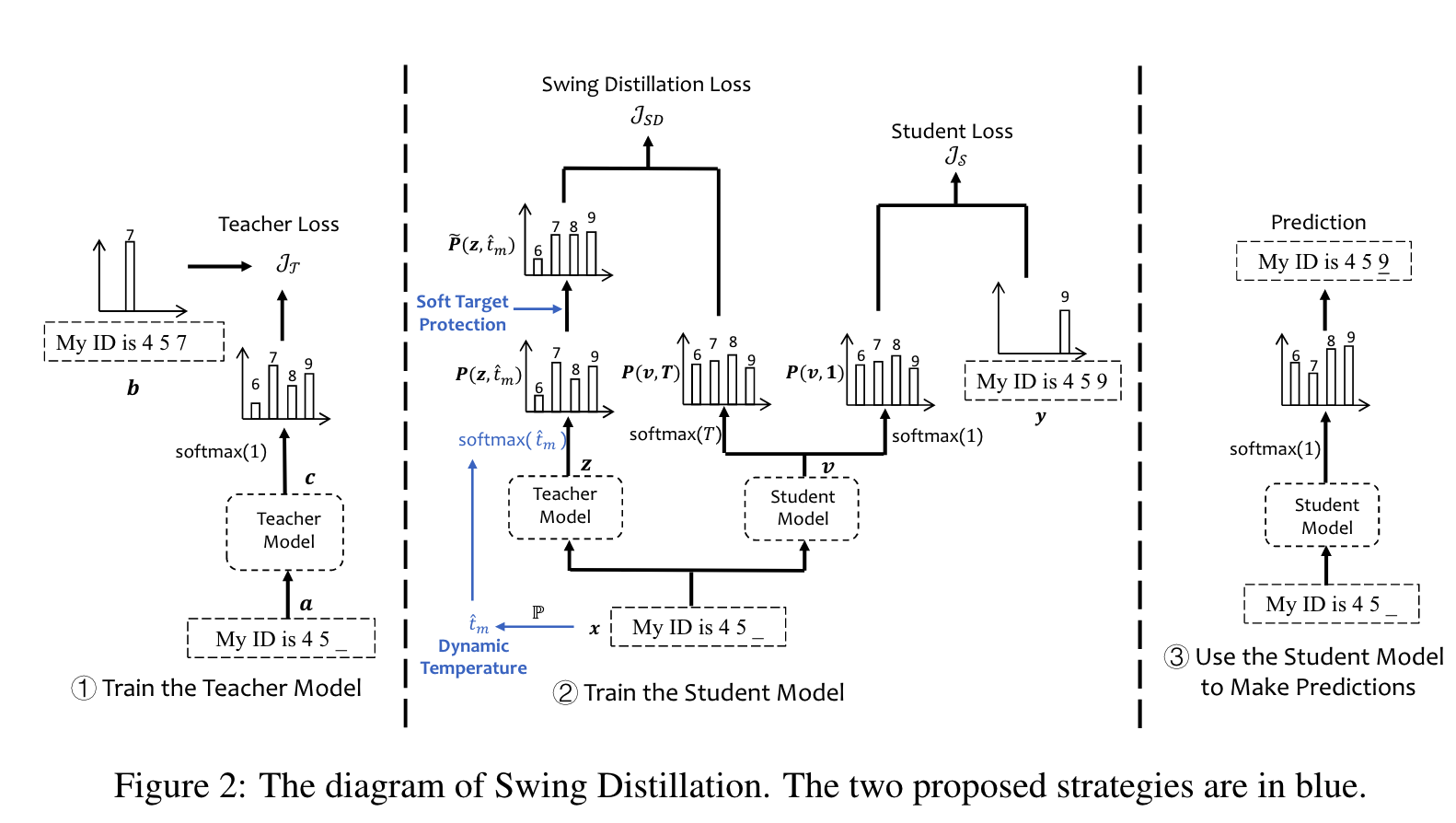

Dynamic Temperature

lower temperature: sharpens the distribution of soft targets, 使得更关注于 logits 较大的分类。
higher temperature：使得分布更加平坦，因此增加了学习的难度。
因此，本文考虑对于 private information 使用一个更高的温度来蒸馏soft targets，对于 non-sensitive soft targets 使用一个更低的温度。
使用自适应的温度系数来控制 soft targets 的传输，teacher model 可以选择性地传输知识给 student model。
private information 的出现通常伴随具体的关键词，比如 name, password 等。这些关键词被认为是识别 private information 的线索。我们构建一个隐私线索词典 $\mathbb{P}$ 来识别哪些信息是不希望传输给 student model 的。
对于给定句子向量 $x = [x_1,x_2,…,x_m]$ ，如果 $x_i$ 是隐私线索词，即 $x_i\in\mathbb{P}$ ,如果 $x_m$ 与 $x_i$ 越近，就说明 $x_i$ 包含了更多的隐私信息。因此，在蒸馏的时候，词 $x_m$ 对应的温度 $\hat t_m$ 计算为：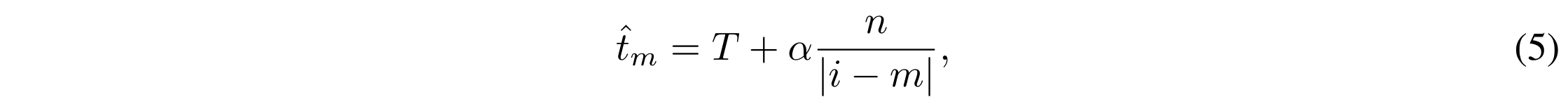

此时的温度不再是一个常数 T，而是一个系数向量 $\hat t\in\mathbb R^n$
在蒸馏的时候，学生数据集的每个输入 $x$ 向量对应的 teacher model 的输出 z 向量 $z = \mathcal{T}(x)$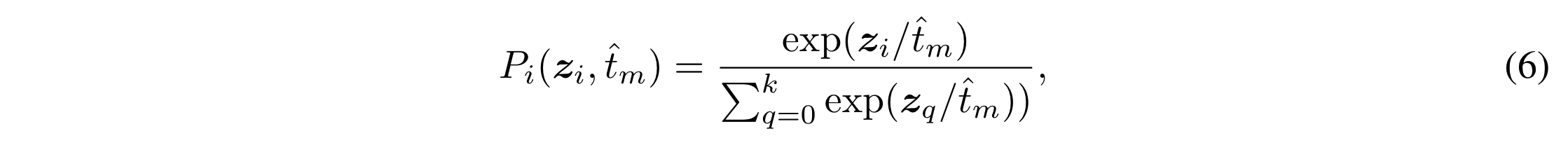

Soft Target Protection

只依靠动态温度调整策略是不足以支持保护隐私信息的，并不是所有的隐私信息都与隐私线索词相关。因此，进一步提出了对 soft target 的保护策略。
向 soft targets 添加 Laplace 噪声：

预测概率主要分布在前几类中。因此，没有必要在每个类别的概率中添加噪声。
本文是对最高概率分布的 $P(z,\hat t_m)$ top-k的分类添加 Laplacian 噪声，得到 :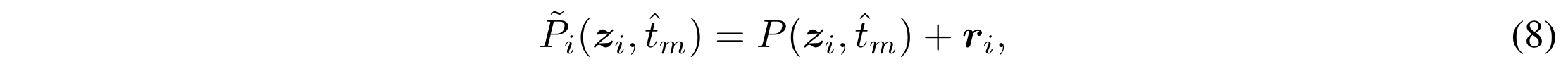

其他类别的概率是不变的，只是对 Top-K 的概率加噪声。

Training and Inference of the Student Model

对于蒸馏过程中的输入 $x$ ，分别输入给 teacher model 和 student model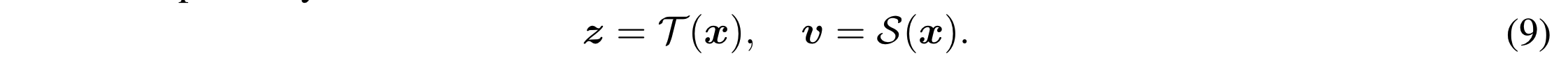

对于学生模型而言，常数 T 的 softmax 的输出结果是可以直接使用的，因为输入的 $x\in \mathbb{S}$, student model 的loss function 表示为：
前一项是 teacher 在动态 T的情况下，选择性加噪之后的结果，后一项是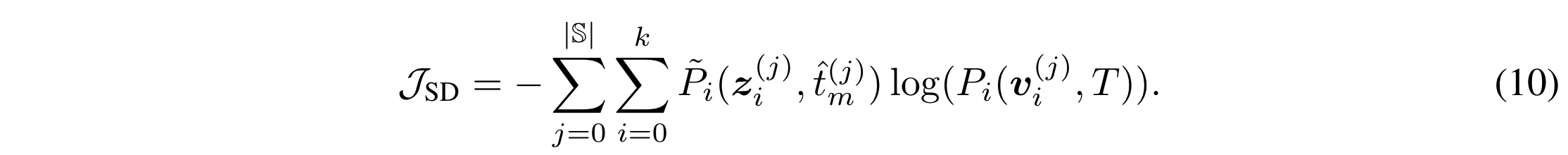

总的训练目标是教师模型蒸馏的 SD 损失和学生模型自学的交叉熵损失的线性插值：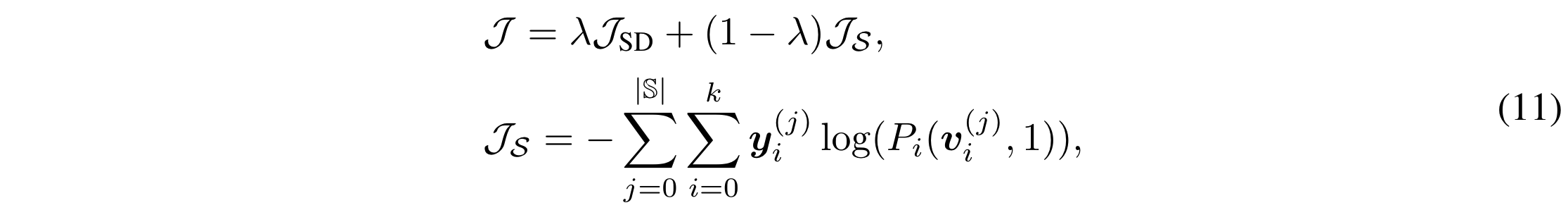

Experiments

Evaluating Privacy-Preserving Capability via Canary Exposure

我们通过在训练数据中插入金丝雀标记/序列来评估保护隐私的能力。我们在训练数据集中插入特殊序列（称为金丝雀）。我们在含有金丝雀的数据上训练模型，并计算插入的金丝雀的曝光率，以衡量模型是否记住了这些金丝雀并将其输出。
给定金丝雀 c、带参数 θ 的模型和随机性空间 R，金丝雀 c 的暴露值 eθ 可计算为：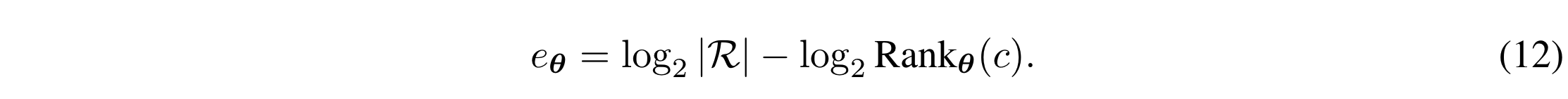

Main Results

与 KD 相比，SD 大幅减少了 80% 以上的金丝雀暴露，这表明 SD 能够显著提高模型的隐私保护性能，而不会对任务性能产生负面影响。学生模型没有插入金丝雀，因此，学生模型的预测结果可以看作是预言机，SD 可以将金丝雀的曝光率降低到这种预言机曝光率。这表明 SD 在隐私保护方面非常有效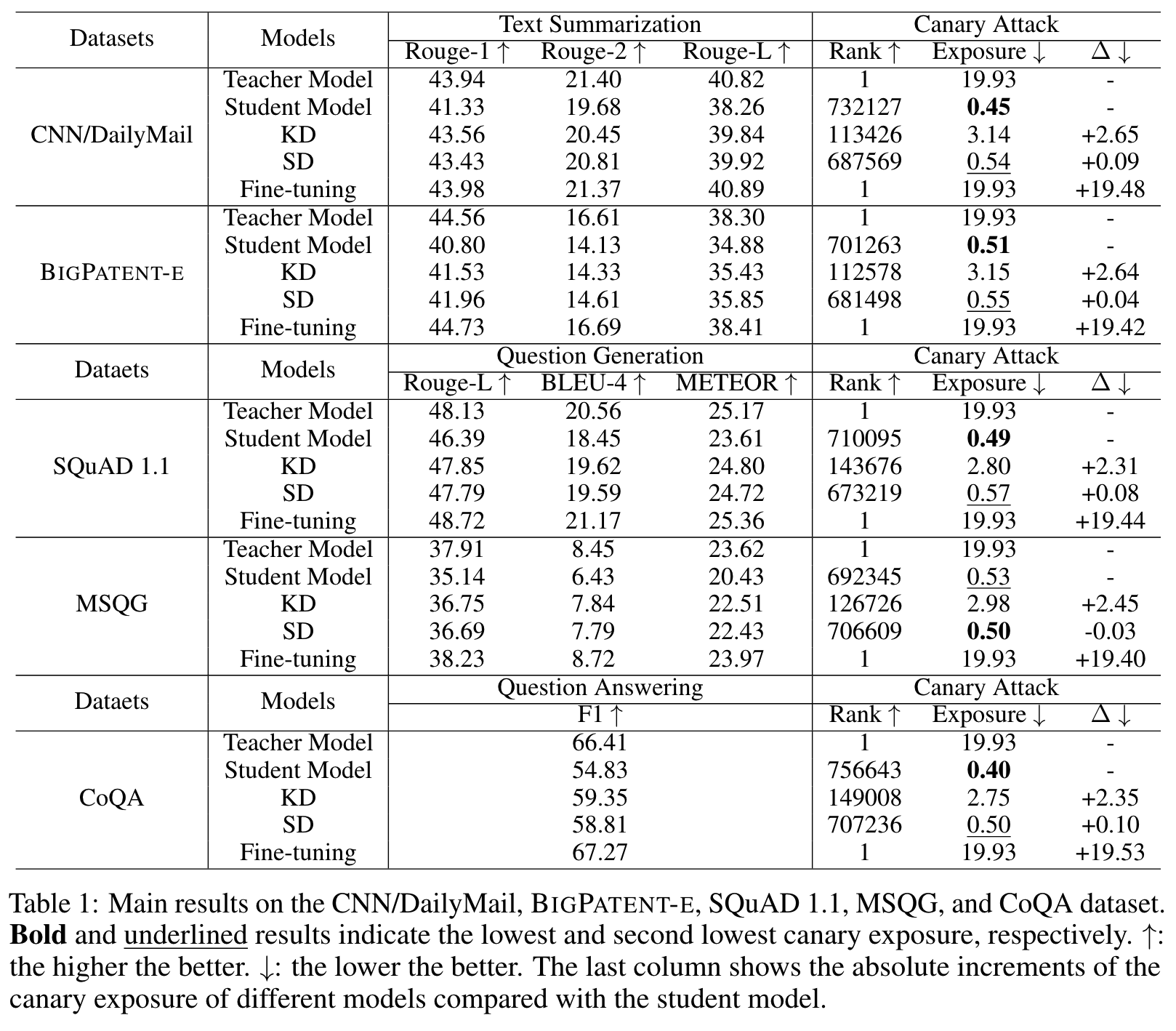

我们发现 KD 的金丝雀暴露率远远高于学生模型和 SD，这进一步验证了知识蒸馏存在隐私泄露问题。
教师模型在所有数据集上的曝光率为 19.93，这也是最大曝光率。这是因为教师模型会记住插入的金丝雀，并在收到对金丝雀敏感的提示时输出金丝雀。虽然在 S 上直接微调教师模型可以提高任务性能，但其暴露值为 19.93，与未微调的教师模型相同。这表明，直接微调有很大的隐私泄露风险（因为微调后的模型仍会记住插入的金丝雀），从而影响微调对任务性能的改善。
我们进行了消融实验，以检验拟议的动态温度（DT）和软目标保护（STP）策略的有效性。”w/o DT “表示在 SD 中不使用动态温度策略，而 “w/o STP “则指不使用软目标保护策略的 SD。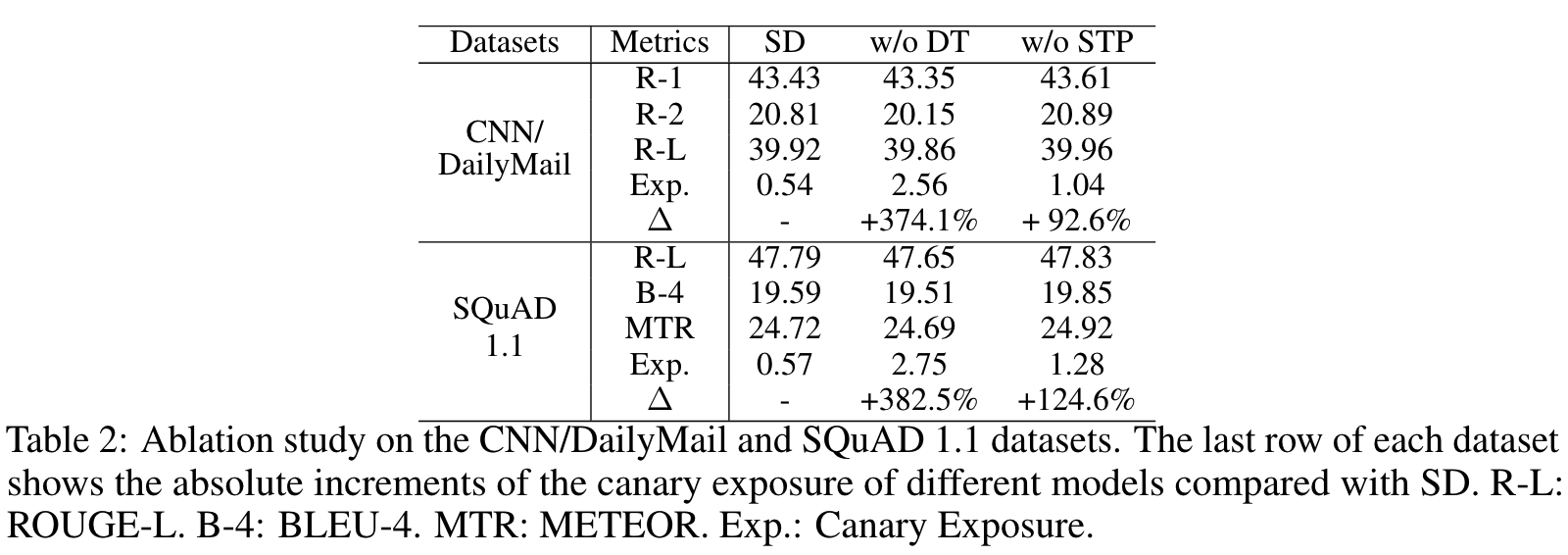

可以看出，从 SD 中移除这两种策略对任务性能的影响非常小（甚至可以获得更好的任务性能）。相比之下，从金丝雀暴露的角度来看，它对隐私保护的影响却非常大。如果不使用动态温度策略，金丝雀暴露率会比标清策略大幅增加 350%以上，而如果不使用软目标保护策略，金丝雀暴露率平均会增加 100%以上。这表明这两种策略对标清隐私保护非常重要，而动态温度策略对隐私保护的贡献几乎是软目标保护策略的三倍。

Injecting Noise of Different Distributions into KD and SD

我们进一步进行了实验，以比较在 KD 和 SD 中注入不同分布（如拉普拉斯分布）的噪声的效果。表 3 报告了结果。KD 和 DT（动态温度）的区别在于前者使用的是静态温度，而后者使用的是动态温度。+拉普拉斯 “与我们的 STP 的区别在于，前者向所有软目标注入噪声，而 STP 只向 Top-K 软目标注入噪声（所有实验中 K 均设为 3）。所有这些方法都使用相同的隐私预算 = 1，这表明隐私保证相对严格。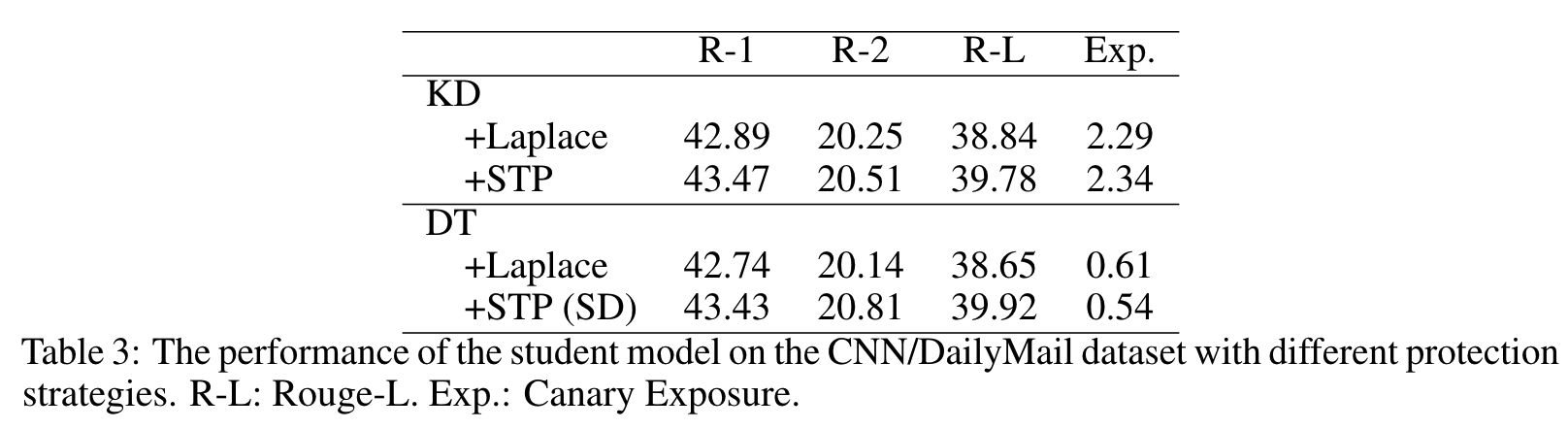

虽然拉普拉斯噪声注入可以减少学生模型的暴露，但它们会显著降低学生模型在相应任务中的性能。特别是与我们提出的 STP 相比，对任务性能的负面影响更为明显
在 KD 中，所有噪声注入策略都能有效减少模型的暴露。然而，金丝雀的暴露量仍然高于学生模型。这再次证明了动态温度策略的必要性和有效性。

传统的方法试图在私人数据上训练一个安全的模型，而我们的目标是防止在私人数据上训练的模型的隐私泄露给学生模型。

Temperature Visualization in SD vs. KD

我们在图 3 中以 SD 与 KD（T=2）为例，将动态温度可视化。这是一封包含 50 个标记的电子邮件，其中第 12 个标记是隐私线索词。
可以看出，SD 的温度会发生相应的变化，而不是像 KD 那样所有标记的温度都保持不变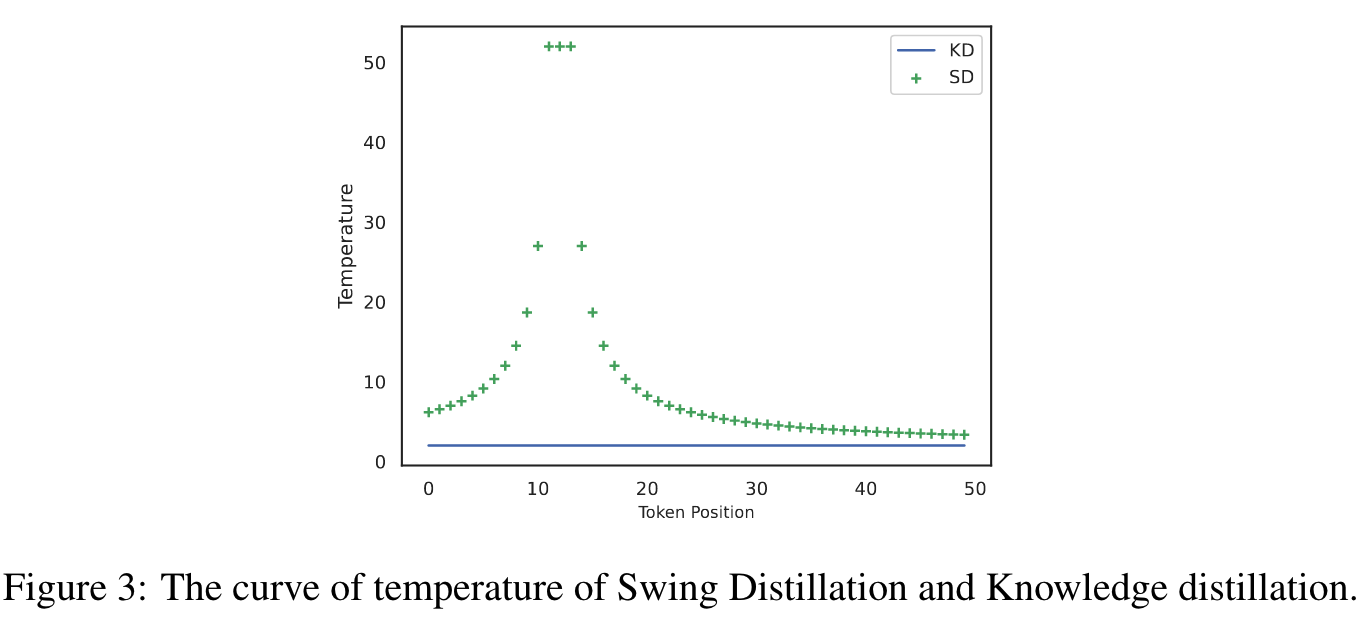

Privacy Clue Word Dictionary $\mathbb{P}$

隐私线索词词典 P 的构建非常灵活，并不局限于传统意义上的私人信息。例如，当蒸馏发生在两个机构之间时，隐私词可能与项目计划、进度、想法等有关。此外，P 的大小对蒸馏效果也有一定影响。如果 P 的大小过大，可能会影响提炼效果。隐私线索词不一定是一个单词，也可以是一些特殊符号，如电子邮件地址中的 @。
在实验中，我们构建了一个大小为 127 的字典 P。它主要涵盖个人信息方面的私人信息，这些信息是从安然公司电子邮件数据集的一个子集中人工提取的。

Conclusion

在本文中，我们通过经验验证了 KD 在教师模型到学生模型的训练数据中存在泄露隐私的风险。为了解决这个问题，我们提出了一种新的蒸馏框架–摇摆蒸馏，其中的温度系数会根据每个实例的隐私情况进行动态自适应调整。此外，为了避免通过软目标泄露隐私，我们进一步提出了通过噪声注入的软目标保护策略。在多个数据集和任务上的实验证明：(1) SD 能够显著减少学生模型的金丝雀暴露，同时保持与 KD 相当甚至更好的任务性能；(2) 这两种策略都能有效保护隐私。