Distilling the Knowledge in a Neural Network
#LLM #Knowledge-Distillation
Metadata
- Authors: [[Geoffrey Hinton]], [[Oriol Vinyals]], [[Jeff Dean]]
- Date: [[2015-03-09]]
- Date Added: [[2023-10-31]]
- URL: http://arxiv.org/abs/1503.02531
- Topics: [[LLM+KD]]
- Tags: #Computer-Science—Machine-Learning, #Statistics—Machine-Learning, #Computer-Science—Neural-and-Evolutionary-Computing, #/unread, #zotero, #literature-notes, #reference
- PDF Attachments
Abstract
A very simple way to improve the performance of almost any machine learning algorithm is to train many different models on the same data and then to average their predictions. Unfortunately, making predictions using a whole ensemble of models is cumbersome and may be too computationally expensive to allow deployment to a large number of users, especially if the individual models are large neural nets. Caruana and his collaborators have shown that it is possible to compress the knowledge in an ensemble into a single model which is much easier to deploy and we develop this approach further using a different compression technique. We achieve some surprising results on MNIST and we show that we can significantly improve the acoustic model of a heavily used commercial system by distilling the knowledge in an ensemble of models into a single model. We also introduce a new type of ensemble composed of one or more full models and many specialist models which learn to distinguish fine-grained classes that the full models confuse. Unlike a mixture of experts, these specialist models can be trained rapidly and in parallel.
Zotero links
Highlights and Annotations
- [[Distilling the Knowledge in a Neural Network - Comment NIPS 2014 Deep Learning Workshop]]
Note
通用方法:多种模型在相同的数据上训练,聚合它们的 predictions。
但是这类方法计算开销大,难以部署在大规模用户上。
提出:compress/distill 一个 ensemble 的 knowledge 到一个 single model。
“distillation” : transfer the knowledge from the cumbersome model to a small mode.
Training:
add a small term, encourages the small model to predict the true targets as well as matching the soft targets provided by the cumbersome model.
Distillation
‘softmax’ as the output layer:
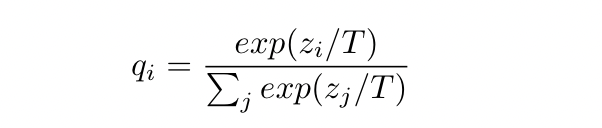
convert logit $z_i$ to a probability $q_i$
T is the temperature. (higher T –> softer probability distribution)
simplest form of distillation:
- large model knowledge –> training on a transfer set –> generate soft target distribution (logits after softmax) –> distilled model
large model logits $v_i$. soft target probabilities $p_i$
small model logits $z_i$, soft target probabilities $q_i$
gradient:
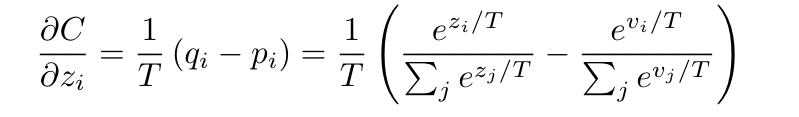
if the temperature high —> 近似 $e^{z_i/T}$ = $z_i/T$
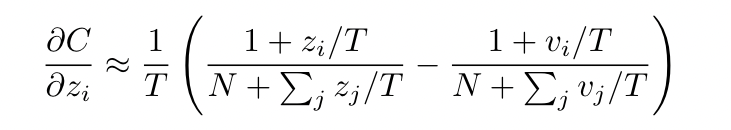
if we assume logits have been zero-meaned (零和)–> $\sum_j z_j = \sum_j v_j = 0$
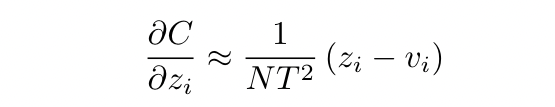
在 temperature 较高的时候, distillation 等价于最小化 $1/2 (z_i-v_i)^2$
在temperature 较低的时候,distillation 更少关注于比平均值更 negative 的 logits, 这是一种正确的做法,因为这种 negative 的 logits 是 noisy。
因此,在模型比较小的时候,temperature 不要太高的效果比较好,可以忽略一些较大的负数logits。

