FetchSGD Communication-Efficient Federated Learning with Sketching
原文来源:[PMLR2020] FetchSGD Communication-Efficient Federated Learning with Sketching
欢迎大家访问我的GitHub博客
https://lunan0320.cn
0. Abstract
Federated Learning 由于 sparse client participation存在的两个问题:
- communication bottleneck
- convergence issues
FetchSGD 使用 linear Count Sketch (计数草图) 压缩 model updates.
将 momentum and error accumulation 从 clients 移到 central aggregator.
1. Introduction
训练 high-quality models 的问题:
1、communication-efficiency
clients 与 aggregator 是一种 low connections.
2、client must be stateless
no client participates more than once during training.
3、not independent and identically distributed
FetchSGD: compress the gradient using a data structure called a Count Sketch.
aggregator: maintains momentum and error accumulation Count Sketches.

experiments:
- image recognition
- language modeling
2. Related Work
2.1 FedAvg
FedAvg 通过在向 aggregator 发送 update 前,先在本地执行多次 SGD 减少了在训练过程中 transfer 的 bytes
FedAvg 是在 federated setting 中最常使用的优化算法
advantage:
(1)no local state,对于 clients 在训练过程中只参与一次是必须的
(2)communication-efficient, reduce the total number of bytes transferred.
disadvantage:
(1)network connections may be too slow or unreliable.
(2)many local steps lead to degraded convergence on non-iid. data. (local over-fitting)
local steps越多,non-iid. 的 convergence 会 变慢
improve performance on non-iid. data:
penalizing the L2 distance between local models and the current global model.
2.2 Gradient Compression
FedAvg limitation:
each round, clients download an entire model (广播)and upload an entire model update. (training large models with FedAvg difficult)
Uploading model updates is challenging. (connections tend to be asymmetric)
Alternative to FedAvg:
gradient compression.
compress stochastic gradients –> the result is still an unbiased estimate of the true gradient.
eg. stochastic quantization, stochastic sparsification.
tradeoff:
compression and the variance of the stochastic gradient.
Biased gradient compression methods:
减少传输的数据量
稀疏化方法通过只上传部分重要的梯度来进行全局模型的更新
梯度的大小来衡量其重要性, 通过预先设立阈值, 当梯度大于该阈值时对其进行上传
固定稀疏率, 每次传递一定比例的最大梯度或每次传递前k个最大梯度的Top-k方法
(1)top-k sparsification (每次传递前k个最大梯度的Topk方法)
(2)signSGD (保留梯度的符号来更新模型, 将负梯度量化为–1, 其余量化为1, 实现了32倍的压缩)
2.3 Optimization with Sketching
- 之前提出的 sketching techniques to optimization,没有收敛性保证,并且 compression little.
而且没有利用 error accumulation, 这对于 biased gradient compression schemes 是 必须的
- sketches for gradient compression in data center training.
在发送完 compressed gradients. requires a second round of communication between the clients and the parameter server.
有的方法需要 local client state for both momentum and error accumulation.
sketches for distributed optimization.
压缩的是 auxiliary variables, eg. momentum, and per-parameter learning rates. 而不是 gradients themselves.
有的方法是 using sketched updates 来实现高效通信, the family of sketches updates, the combination of subsampling, quantization, and random rotations.
本文的方法:compress the gradients and do not require any additional communication at all to carry out momentum.
3. FetchSGD
3.1 Federated Learning Setup
C clients, Z 是 data domain
supervised learning:
$ Z = X \times Y$, X 是 feature space, Y 是 label space.
unsupervised learning:
$Z = X$, X 是 feature space.
第 i 个 client 有 $D_i$ samples, 从 $P_i$ 中提取出的 i.i.d.
设 W 是由 d dimensional vectors 参数化的假设类
目标:minimize the weighted average (加权)

the average of client risks:

3.2 Algorithm
FedSGD的每次迭代,第 i 个 participating client 计算 a stochastic gradient $g_i^t$ 使用 local data 的一个batch.
使用 Count Sketch data structure compress $g_i^t$
每个 client 发送 $S(g_t^t)$ 给 aggregator 作为 model update.
Count Sketch:
一种随机的数据结构,将一个 vector 投影几次,到一个较低维度的空间来压缩它,之后就可以大致恢复 high-magnitude elements(高量级元素)
Count Sketch 满足如下的 linear property:
$$
S(g_1+g_2) = S(g_1) + S(g_2)
$$
这样的线性关系使得 server 可以准确计算
$$
\sum_i S(g_i^t) = S(\sum_ig_i^t) = S(g^t)
$$
对于一个 sketching operator $S(·)$,都有与之对应的 decompression operator $U(·)$,返回的是 original vector 的unbiased estimate
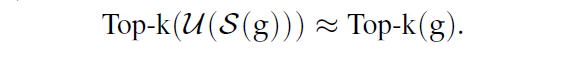
$U(·)$其实是对 $S(·)$ “undoes” the projections.
持有 $S(g_i^t)$时,central aggregator 可以 update the global model:
$$
Top-k(U(\sum_iS(g_i^t))) \approx Top-k(g^t)
$$
biased gradient compression methods can converge:
biased gradient compression operator 累积了 error
并在 optimization 过程中重新引入了 error.
在 FetchSGD,bias 是由 Top-k 引入的而非 $S(·)$
因此,aggregator 可以 accumulates the error.
zero-initialized sketch $S_e$

$\eta$ 是 learning rate,$\triangle^t\in R^d$ 是 $k-sparse$
对比:
其他的 biased gradient compression methods 在 compress the gradients 时候在clients 引入了 bias, 因此需要在 clients 保持独立的 error accumulation vectors. (在 clients 端,计算压缩误差存储在本地,在下一轮被选中训练时,进行梯度修正)
但这对于 Federated learning 是比较难的,因为 clients 可能只参与一次,使得 error 无法在之后的 round 中被引入。
Another View:
$S(·)$ 是linear, error accumulation 只是由 linear operations 组成,使用$S_e$在 server 执行 error accumulation 与在 client执行 error accumulation 是等价的
而且 momentum 也是由 linear operations 组成,因此 momentum 也可在 clients 或者在 server执行。

FetchSGD is presented in full in Algorithm 1.

4. Theory
FetchSGD convergence guarantees
4.1 Scenario 1: Contraction Holds
biased gradient compression operator 可以使得 compressed SGD converge
已经存在的方法证明了 compressed SGD converges, 当 $C$ 满足 $\tau-contraction$
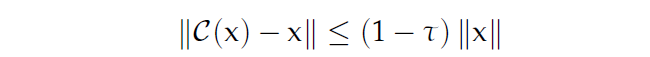
已有的证明证实:使用 Count Sketches 去压缩梯度可以满足上述特征
但是这个压缩方法包括
1、一个 second round of communication.
如果由$S(e^t)$计算的$e^t$中没有high-magnitude 高量级 elements,server可以随机查询$e^t$
2、FetchSGD 不计算$e_i^t$ 或者 $e^t$, 因此 第二轮的通信是不可能的,现有的方法是行不通的。
Assumption 1 (Scenario 1)
${w_t}_{t=1}^T$ 是 FetchSGD 生成的 models 的 sequence
${u^t}{t=1}^T$ 和 ${e^t}{t=1}^T$ 是 momentum 和 error accumulation vectors.
存在常数 $0 < \tau < 1$, 对于任意的$t\in[T]$, $q^t := \eta (\rho u^{t-1}+g^{t-1})+e^{t-1}$, 在满足 $\tau||q_i^t||^2\leq(q_i^t)^2$的情况下,至少有一个 coordinate.
Theorem 1(Scenario 1)
$f$ 是一个 $L-smooth\quad non-convex\quad function$ , 并且有上界 G
L-smooth 的定义:
在 Assumption 1的情况下, FetchSGD 在步长 $\eta = \frac{1-\rho}{2L\sqrt{T}}$ 执行T 轮,返回 ${w^t}_{t=1}^T$,在概率至少 $1-\delta$ sketching randomness: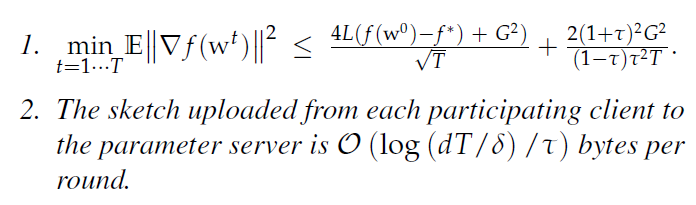
第一部分的期望,是在 mini batches sampling 的随机性
对于更大的 T ,第一项占主导地位, Theorem 1 中的收敛率与在 uncompressed SGD 情况下的匹配。
Assumption 1 缩放了 negative gradient,以及 momentum、error accumulation vector必须指向完全相同的方向
下一小节分析在只包括 gradients 下的假设下的 FetchSGD
4.2 Scenario 2: SlidingWindow Heavy Hitters
沿着 optimization path 的 gradients 已经被观察到包括heavy coordinates.
但是假设 all gradients 包括 heavy coordinates 是有些过度optimistic, 因为在一些平坦的参数空间可能不是这样
更加缓和的 assumption: 在 gradient vectors 的 sliding sum中存在 heavy coordinates.
Definition 1
[$(I,\tau)-sliding\quad heavy$]
stochastic process ${g^t}_{t\in N}$ 是 $(I,\tau)-sliding\quad heavy$, 如果在每次迭代 t 中,有至少 $1-\delta$ 的概率,gradient vector $g^t$可以分解为 $g^t = g_N^t+g_S^t$,其中 $g_S^t$ 是 “signal” ,$g_N^t$ 是 “noise”:
- signal
对于vector $g_S^t$,每个 non-zero coordinate j,满足如下:

- noise
$g_N^t$ 是均值为0,对称,且使用范数规范化, second moment bounded as:

如果将连续的 $I$ 个 gradients sum up,结果中的每个坐标要么是 $\tau-heavy\quad hitter$,要么是从一些 mean-zero symmetric noise 提取出的
Count Sketches 可以捕获 signal,因为 Count Sketch 可以近似于 heavy hitters.
signal 分布在大小为 $I$ 的 sliding windows, 需要一个 sliding window error accumulation scheme, 来确保可以捕获到任何时刻的 signal.
Vanilla error accumulation 不足以显示 convergence
vanilla error accumulation 是 all prior gradients的累积,仅有在 $I$ consecutive gradients 的 sum up中的signal 不会被 vanilla error accumulation 捕获
因此考虑使用 sliding window error accumulation scheme,可以捕获任何在 $I$ 个sequence 的 gradients
simple way:
保持 $ I $ error accumulation Count Sketches,如下图所示,是 $ I =4$ 的情况,每次迭代时,每个 sketch accumulates新的 gradients,在继续积累梯度前,每 $I$ 次迭代时,sketch就会被归零

每次迭代时,都有一个 sketch available,包括了 prior $I’$ gradients, $I’\leq I$
实际中,保持 I error accumulation sketches 是 too expensive
但是,“sliding window” 被广泛研究,通过 $log(I)$ error accumulation sketches 就可以识别 heavy hitters.
Assumption 2 (Scenario 2)
优化过程中的遇到的梯度序列,是一个 $(I,\tau)-sliding\quad heavy$ stochastic process.
Theorem 2(Scenario 2)
f 是一个 L-smooth non-convex function
$g_i$ 代表了 $f_i$ 的 stochastic gradients,使得 $||g_i||^2 \leq G^2$
在 Assumption 2下,FetchSGD 使用 a sketch size $O(\frac{log(dT/\delta)}{\tau^2})$,步长是 $\eta = \frac{1}{G\sqrt{L}T^{2/3}}$, $\rho = 0$ 代表 no momentum,满足概率至少 $1-2\delta$,返回 ${w^t}_{t=1}^T$,使得:
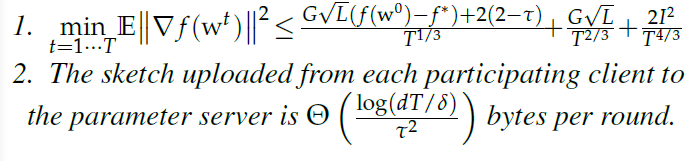
定理第一部分的期望是关于小批次抽样的随机性
Remarks
- 这些是在 non-i.i.d.设置下的guarantees, f 是 对于可能不相关的分布的 average risk.
- 收敛速度限制了目标梯度范数,而不是目标本身
- 定理1 中的收敛速度与 uncompressed SGD 收敛速度相匹配,而在Theorem 2中情况更差
- proof 使用了 virtual sequence idea,可以被泛化到其他类的函数:smooth、(strongly) convex etc.
5. Evalauation
实现并比较 FetchSGD、gradient sparsification (local top-k)、FedAvg。
使用 neural networks with ReLU activations, loss surfaces are not L-smooth.
使用 a vanilla Count Sketch, 而不是 a sliding window Count Sketch
使用 non-zero momentum,这是 Theorem 1 allows,但是Theorem 2 不允许的
使用 momentum factor masking
对于在 $S_e^t$中的 $S(\triangle^t)$的 nonzero coordinates zero out, 而不是减去 $S(\triangle^t)$
实验针对于 small local datasets and non-i.i.d. data
Gradient sparsification 方法,是对每个 worker 的 local top-k elements求和,当local datasets变得更小,而且彼此间差异越大时,在逼近global gradient的真实 top-k 上的效果更差
在每个 client 的 local data 上执行多步骤,效果也并不好,因为这会直接导致 local overfitting.
而且真实情况下,most users 是相对小的数据集,真实的data在 FL中也是 non-i.i.d.
FetchSGD advantage
compression operator is linear. 小的数据集也不会造成困难,使用 N个数据点的单个client 执行一个步骤,等同于使用 N 个clients 在单个数据点上执行一个步骤。
non-i.i.d. 的问题可以通过随机选择 clients 来缓解 (FedAvg 加权)
在FedAvg中,clients 在参与之前必须下载整个 model,因为模型的每个 weight 都会在这一轮更新
local top-k and FetchSGD 每轮只更新一定数量的参数,而不参与的 clients 就可以保持当前的 model,这就减少了参与前下载的参数的数量
因此,对于local top-k and FetchSGD,upload compression 比 download compression 更重要。
- FedAvg 是通过减少迭代的次数来实现 compression 的,因此只要放缩 learning rate,来匹配 FedAvg执行的迭代总数
在non-federated setting 中,momentum 是很重要的,可以实现更好的性能
在federated learning,momentum 是 clients 在local gradients上执行,这对于 clients 只参与一次或几次是没影响的。
而 central aggregator 可以执行 momentum 在聚合模型更新时,但是对于FedAvg 和 local top-k ,momentum 没有更好的效果,而 FetchSGD由于 compression operator linearity能够无缝衔接 momentum
5.1 CIFAR(ResNet9)
CIFAR10 和 CIFAR100 是 image classificaion datasets
如图所示是在 CIFAR10 和 CIFAR100 上的 test accuracy vs. compression

5.2 FEMNIST (ResNet101)
Federated EMNIST 是 an image classification dataset, 62个类别 (大小写字母加数字)
在 low compression, FetchSGD outperforms the uncompressed baseline.
observation: local top-k 使用 global momentum 显著地 outperforms other methods on this task.

5.3 PersonaChat(GPT2)
GPT2-small model, a transformer model, 用于 language modeling.
在 PersonaChat dataset(a chit-chat dataset)上预先训练 GPT2
在 validation dataset 上测试了 perplexity (语言模型的标准度量,越低越好)
右侧是 loss curves(negative log likelihood), 所有的 compression techniques 在早期都优于 uncompressed baseline,但是大多数都过早饱和,这时压缩引入的错误开始阻碍训练。

6. Discussion
FL 在 communication efficiency 方面引起了极大的关注
之前的工作是为了减少 在达到收敛前所需的 total number of communication rounds,没有减少每一轮中所需要的通信量
本文引入 FetchSGD算法,在符合 FL 其他约束条件的情况下,减少了每轮的通信量
FetchSGD 很容易解决 non-i.i.d. data的问题,这对于其他的方法可能是很复杂的
FL 未来研究也是针对结合轮数的效率和每轮的效率进行优化。



